Progressive Pathways
Part of my conviction that games can work well for teaching is a theory of instruction related to the Socratic method. It is the idea of presenting an argument as a series of questions or exercises, first of specific cases, then of generalizations. R. P. Burn's A pathway into number theory is made up entirely of questions, and explains the approach as follows:
This book on number theory has been put together by keeping a record of how I actually resolved the blocks which I encountered as I read a number of standard texts. Time and again, it was the exploration of special cases which illuminated the generalities for me. This collection of explorations was then organized into a sequence in such a way that the 'pathway' would climb towards the standard theorems which occur here as problems for the student at the end of each section.
This "block resolution" approach is interesting; I consider it related to the theory of impasse-driven learning advanced by VanLehn (and previously mentioned towards the end of this post). By combining questions likely to provide impasses with the programmed learning conceit of immediate feedback, the learner's inductively-developed understanding of the system ought to be improved. I admit that VanLehn's concept of impasse isn't quite a perfect match, not to mention relating to much simpler algorithms, but I think there is some resonance between the two.
Daniel P. Friedman's The Little LISPer is also presented as questions and answers (though much closer together than Pathway gives its answers), in this case as an introduction to Lisp. From the 1974 edition's introduction:
DO NOT HESITATE TO GUESS. This book is based on intuition, and yours is as good as anyone's. We expect you to guess. Occasionally we make you guess before giving the answer, either because we do not expect you to know an answer at a particular stage, or because we want you, in case you guessed wrongly, to slow down and look back for what you missed earlier.
Both authors also call out a particular lack of formality, and not just due to each being an introductory text. From the preface to the second edition of Pathway:
The central point of the Pathway is to enable students to participate in the formulation of central mathematical ideas before a formal treatment (which, suitably introduced, they may well be able to provide themselves).
and from LISPer:
No formal definitions are given in this book. We believe that you can form your own definitions and will thus remember them and understand them better than if we had written each one for you.
Sadly I can't vouch for the effectiveness of either of these books. Despite starting on it several times, Pathway quickly becomes too notation-heavy for my math-weak mind. Running through LISPer without a computer renders it a rather sterile exercise, although the book does not recommend a computer companion (though this may be due to the scarcity of computer resources when it was written). Pathway does recommend a calculator, but my TI-83 hasn't proven terribly helpful so far. I think that a game can be more successful here, with a more experimentation-friendly interface and better integration between the problems and the rule system (as in my earlier post).
Continuity is my favorite example of using a well-crafted level progression to teach. Levels are made up of a number of sliding tiles (or slides), as in a fifteen puzzle. In one mode you simply slide these tiles around. Pressing the spacebar toggles to another mode, in which you play a platformer set in the level formed by the tiles. It is a very smooth introduction: level 1 doesn't require the sliding mechanic at all, and level 2 illustrates it in the simplest possible way. Initially it looks like:
But with a single slide, you get:
Once in the latter state, you can toggle to platformer mode and walk the little guy from the left to the right across the gap, to get to the red door which you need to finish the level.
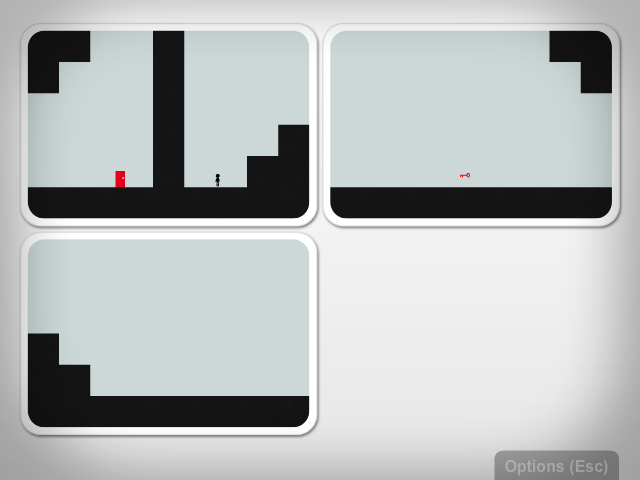
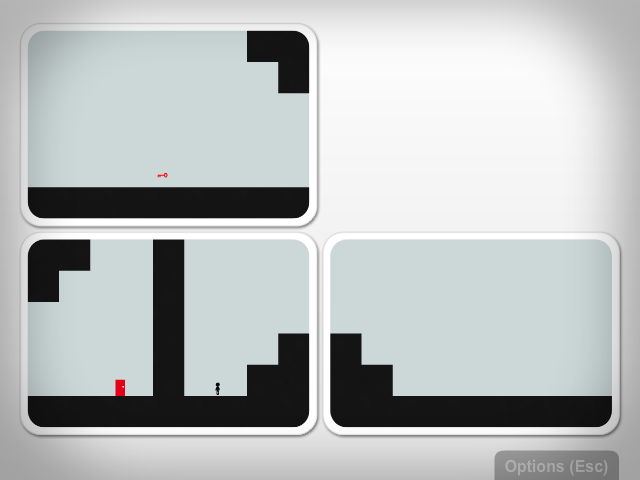
An important complication is that you can only move between tiles when their edges match up completely. This is so important that the game dedicates two early levels to demonstrating it. Here's level 4, initially:
It looks like the easy solution is to go right and grab the key (which you need to get through the door). If you jump up the stairs, though, you run up against the edge and the game buzzes annoyingly. You must rearrange the tiles so that there is a matching staircase on the other side before you can pass through that edge:
You must make several similar moves to complete this level (note the seemingly uninvolved block at the top of the left two tiles, this must also match to pass those edges). I was struck with the elegance of this approach, however it may be a little too subtle. I watched a few people play the game and some of them didn't gather that the matching of edges was the important issue; it seemed to them that the restrictions were arbitrary. One way to clear this up might be a better indication of why nonmatching edges don't match, maybe a highlight of the inequal parts of each.
As well done as this is, and I could spend many posts discussing what I like about Continuity's design, the game only uses this teaching to lead up to the hard puzzle parts that come later. While the mastery of discontinuous space is interesting, I hope to use similar techniques to explore computational spaces as well. It was a direct inspiration for my own prototype A Change of Plans, and while that doesn't hit any terribly interesting concepts either, it emphasizes another advantage of games over textbooks using this method: games naturally support a great variety of solutions.